問題 : 甲乙二人進行一次一元,不輸光不停止的賭博,甲原有 m 元本錢,乙原有 n 元本錢,甲贏一次的機率為 p ,乙贏一次的機率為 q,問甲將乙贏光的機率為多少?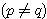 這個問題使筆者想起二十多年前數學傳播中的一個“醉漢回家”問題,題目是一個醉漢喝得不知方向,向前走一步的機率為 p ,後退一步的機率當然就是 1- p ,醉漢距離家有 n 步,但後方 m 步有懸崖,則醉漢摔死的機率為多少?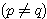 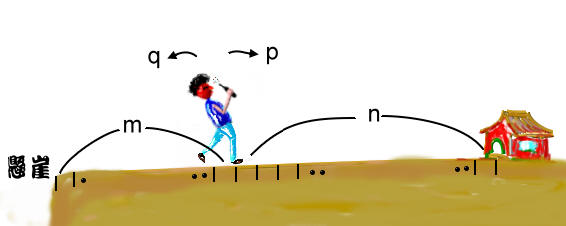 這個機率問題並不簡單,它不能以一般機率方法(分路徑討論)來求機率,因為路徑有無限多種,所以必須用另外的方法解決 考慮路徑 a 到 b ,x 為介於 a 到 b 之間的整數 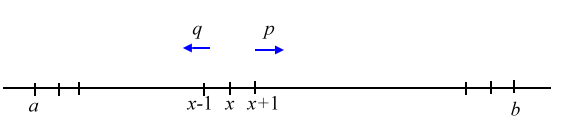
設 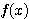 表示目前在 表示目前在 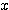 點而到達 b 的機率(讓乙輸光光) 點而到達 b 的機率(讓乙輸光光) 我們還知道 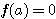 (甲先輸光,那贏光乙的機率=0) (甲先輸光,那贏光乙的機率=0) 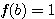 (已經讓乙輸光了,那贏光乙的機率=1) (已經讓乙輸光了,那贏光乙的機率=1) 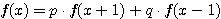 (下一步只有這兩條路,不是輸就是贏) (下一步只有這兩條路,不是輸就是贏) 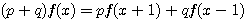 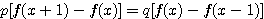 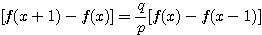 那麼 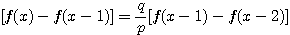 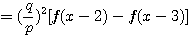 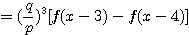 : : 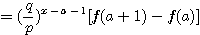 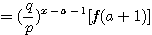 為了方便,我令 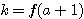 得 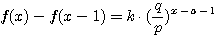 現在列出下列式子在相加 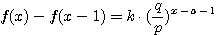 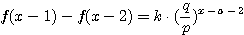 : : + 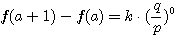 __________________________________________________________ 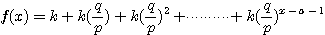 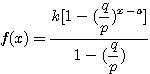 又因 又因 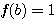 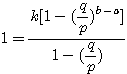 則 則 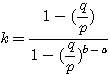 我們求出了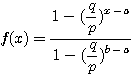 這個公式套用至前面的問題 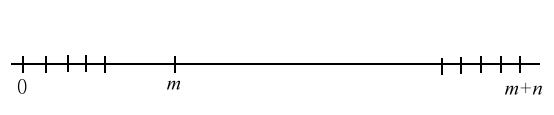
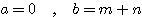 故問題的答案為 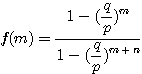 以圖形表示(縱軸表示贏光乙的機率,橫軸表目前甲的本錢)  | | 藍線代表 p = 0.6 紅線代表 p 接近0.5 黑線代表 p = 0.4 三線交會處的 x 座標為m+n |
| 

