| 假設每一對大兔子每月會生一對小兔,每一對小兔每月會成長成大兔,如果不考慮死亡,由一對大兔開始,一年後會有幾之大兔?這是由13世紀義大利數學家費布納西首先提出的有趣問題 我們將這個數列以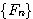 來表示,現在來考慮 來表示,現在來考慮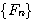 的變化 的變化 一開始為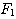 對,一個月後 對,一個月後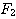 對,二個月後 對,二個月後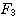 對,n 個月後 對,n 個月後 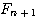 對 對 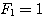 , , 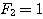 (一個月後一對大兔一對小兔) , (一個月後一對大兔一對小兔) , 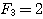 (一對小兔長大了, 老兔又生小兔) , (一對小兔長大了, 老兔又生小兔) , 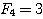 (第二代小兔生小兔) , ........... (第二代小兔生小兔) , ........... 我們得到數列 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21...............其中遞迴關係為 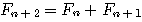 當 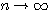 時 , 時 ,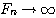 是無庸置疑的,但前項和後項的比值卻是趨近一個定數,就是黃金數 是無庸置疑的,但前項和後項的比值卻是趨近一個定數,就是黃金數 說明: 由上式 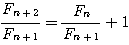 ,兩邊 n 趨近 ,兩邊 n 趨近 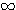 ,(假設極限存在並叫做 k ) ,(假設極限存在並叫做 k ) 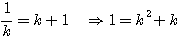 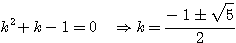 (負不合) (負不合) 左圖紅色大點為大兔,黃色小點為小兔,費布納西數列就是這樣生成的,這種生長關係,和右圖樹枝是不是有點像? |


