
 |
歐千郁的學習歷程 - 111-1計算機概論 - 計算機組織與結構 |
|
|
|
|
計算機組織與結構一個筆記性質的文章,想到什麼寫什麼。
什麼是UTF-8?與Unicode的差別?
計算機的基本儲存單位是「位元(bit)」,通過開關變化設置表達值0或1。在有兩個位元的情況下可以得到四個不同的狀態: 00 01 10 11 如果有三個位,則有八種狀態: 000 001 010 011 100 101 110 111 每當增加一個位時,將得到兩倍的狀態。 電腦常以8個位元為存取單位,因此8個位元稱為「位元組(byte)」。 計算機常用單位  在計算機世界中 A-B = A+(-B) 那你可能會好奇,減法直接減就好了,為什麼要用加法計算減法? 那是因為加法需要「加法器」,那麼減法也就需要「減法器」。 對於早期的機械計算設備而言,加法器是依靠「齒輪」等機械器件實現的。如果人們強行實現減法器,則需要在同一台設備中增加更多齒輪、軸承、連杆等機械器件,導致設備體積增大、成本上升、故障率升高,這是不划算的。 類似的,對於現代數字電子計算機(各種電腦)來說,雖然其體積遠比當年的機械計算機小,但增加一個「減法器」,將要求工程師在晶片上增加更多電晶體以及相關電路,這會增大晶片面積、功耗和一系列開銷,導致晶片成本升高。 因此,為了降低不必要的成本,工程師和科學家想了一招: 能否將加法和減法都統一於「加法」? 這樣一來,只需一台擁有「加法」功能的機器,就可以既算加法,也能算減法。 這就是人們在計算機底層使用補碼的原因。 有號數表示法而常見的有符號數表示法有以下幾種: sign & magnitude(S&m)分配一個符號位(sign bit)來表示這個符號:設定這個位(通常為最高有效位)為0表示一個正數,為1表示一個負數。 數字中的其它位指示數值(或者絕對值)。因此一個位元組只有7位(除去符號位),數值的範圍從0000000(0)到1111111(127)。這樣當你增加一個符號位(第八位)後,可以表示從−127(10)到+127(10)的數字。 這種表示法導致的結果就是可以有兩種方式表示零,00000000(0)與10000000(−0),這大大增加數位電路的複雜性和設計難度。CPU亦須執行兩次比較,來測試運算結果是否為零。  Ones’ complement一個負數的二進位數一補數形式為其絕對值部分按位元取反(即符號位不變,其餘各位按位元取反)。同原碼表示一樣,0的一補數表示形式也有兩種:00000000(+0)與11111111(−0)。 舉例來說,原碼10101011(-43)的一補數形式為11010100(−43)。有符號數用一補數表示的範圍為−(2^(N−1)−1)到(2^(N−1)−1),以及+/−0。一個慣常的八位的位元組便是(可表示)−127(10)到+127(10),以及00000000(+0)或者11111111(−0)。 溢位需做端迴進位。
二進位 十進位
11111110 -1
+ 00000010 +2
..........................
1 00000000 0 <-- 錯誤答案
1 +1 <-- 加上進位
..........................
00000001 1 <-- 正確答案 Two’s complement迴避了0有多種表示的問題以及迴圈進位的需要(溢位不需要做端迴進位)。 在二補數表示中,負數以位元型樣表示為正值的一補數加1(當作無符號數)。 在二補數表示中,只有一個0(00000000)。求一個數的二補數(無論是負數還是正數)需要反轉所有位,然後加1。 可藉由最後一bit是否為1判斷是否為奇數。  下表列出了 4-bit 二進數所能表示的整數:

浮點數表示法實數(Real)包含整數部分和小數部分的數值,例如23.7是一個實數,整數部分為23,小數部分是0.7。位數不足會造成精確度及正確度誤差。 在浮點數表示法中,一個數值是由三個欄位組成:「符號」非正即負;「位移量」顯示小數點應從實際數值往左或右移多少單位(指數形式);「定點數」小數點位置是固定的。 科學記號(Scientific Notation)浮點數表示法的一種。   正規化(Normalization)將數值轉為小數點左方僅有一個非零數字。 * 十進位科學記號: ± d.xxxxxxxx (d = 1 ~ 9, x = 0 ~ 9) * 二進位浮點數: ± 1.yyyyyyyy (y = 0, 1) 符號、指數和尾數* 二進位浮點數儲存 3 項資訊:符號、指數、和尾數 * 例如:+1000111.0101 → +1.0001110101×26 → 儲存:符號(+)、指數(6)、及尾數(0001110101) * 符號:使用一個位元(0, 1)表示 * 指數:使用超碼表示法(Excess) * 尾數:使用定點數表示法 超碼系統(Excess system)* 將整數加一個偏移值(Bias):2^(m–1) –1 (m 為儲存指數的記憶體大小) → 正負整數均轉為正整數  # 例如: – m = 8 (偏移=127):超 127 系統(Excess_127 system) – m = 11 (偏移=1023):超 1023 系統(Excess_1023 system) * 表示程序: # 將指數加上偏移值 # 將結果轉為二進位,若位元<m,左邊補 0 直到位元=m * 例如,以 Excess_127 系統表示–25(10): → –25 + 127 = 102 → 110 0110 → 0110 0110 * 為何使用超碼系統來表示指數? # 將兩個浮點數相加或相減時,指數僅用於比較大小(不需相加或相減) → 不需要使用 2 補數 # 超碼系統都是正數 → 比較大小較為快速(不需考慮正負數) IEEE 754標準 單倍精準數 給定一實數10110.100011,先轉換成1.0110100011*2^4,因為是正數,所以符號位元為0,其尾數部分為小數點後0110100011,指數部分為4,以超127方式儲存,因此將指數部分加上127 = 4+127 = 131,再將131轉為二進位得10000011。 也可以透過轉換後的推回原來的數值,例如0 10000101 00101000110000000000000所儲存的數值為多少? 單精度與倍精度的差別 為了讓誤差更小,IEEE 754 也定義了如何用 64 bit 來表示浮點數,跟 32 bit 比起來 fraction 部分大了超過兩倍,從 23 bit 變成 52 bit,所以精準度自然提高許多 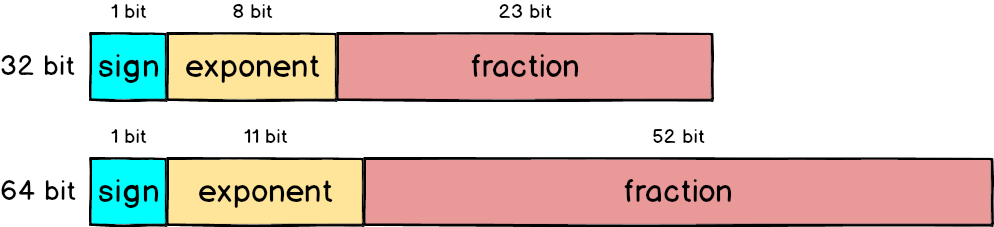
|
|
||||||||||||||||||||||||||
| 中華科技大學數位化學習歷程 - 意見反應 |  |